Longitude And Latitude In Mathematics Pdf

• Home
• High School Notes
• Past Papers
• Primary School Materials
• Schemes of Work

Longitudes and Latitudes - Mathematics Form 4 Notes

Download PDF for future reference Install our android app for easier access

• Introduction
• Great and Small Circles
  • Latitude
  • Longitudes/meridians
• Position Coordinates
• Great Circle Distances
• Distance Along a Small Circle (Circle of Latitude)
• Shortest Distance Between Two Points on the Earths Surface
• Longitude and Time
• Speed
• Past KCSE Questions on the Topic

Introduction

• Just as we use a coordinate system to locate points on a number plane so we use latitude and longitude to locate points on the earth's surface.
• Because the Earth is a sphere, we use a special grid of lines that run across and down a sphere.
• The diagrams below show this grid on a world globe and a flat world map.

Great and Small Circles

• If you cut a 'slice' through a sphere, its shape is a circle.
• A slice through the centre of a sphere is called a great circle, and its radius is the same as that of the sphere. Any other slice is called a small circle, because its radius is smaller than that of a great circle.Hence great circles divides the sphere into two equal parts

Latitude

• Latitudes are imaginary lines that run around the earth and their planes are perpendicular to the axis of the earth.
• The equator is the latitude that divides the earth into two equal parts.
• Its the only great circle among the latitudes. The equator is 0°.
• Theangle of latitude is the angle the latitude makes with the Equator at the centre, O , of the Earth.
• The diagram shows the 50°N parallel of latitude. Parallels of latitude range from 90°N (North Pole) to 90°S (South Pole).
• The angle 5 0 ⁰ subtended at the centre of the earth is the is the is the latitude of the circle passing through 5 0 ⁰ north of equator.The maximum angle of latitude is 9 0 ⁰ north or south of equator.

Longitudes/Meridians

Position Coordinates

• Locations on the Earth are described using latitude (°N or °S) and longitude (°E or °W) in that order.
• For example, Nairobi has coordinates (1°S, 37°E), meaning it is position is 1° south of the Equator and 37° east of the prime meridian.

Example

Sydney's coordinates are (34°S 151°E) while Tokyo's are (35°N, 139°E).

1. Find their difference in latitude.
2. Find their difference in longitude.
3. Which city is further west?

Solution

It is useful to draw a rough grid to position the cities.

1. Difference in latitude = 35° + 34° = 690 Difference between 35 N and 34 S.
2. Difference in longitude = 151° - 139° = 12° Difference between 151°E and 139°E.
3. Sydney is further east, so Tokyo is further west.

Great Circle Distances

• Remember the arc length of a circle is where θ is the degrees of the central angle, and the radius of the earth is 6370 km approx.
• On a flat surface, the shortest distance between two points is a straight line.
• Since the Earth's surface is curved, the shortest distance between A and B is the arc length AB of the great circle that passes through A and B . This is called the great circle distance and the size of angle ∠ AOB where O is the centre of the Earth is called the angular distance.
  Note
  • The length of an arc of a great circle subtending an angle of 1 ⁱ (one minute) at the centre of the earth is 1 nautical mile nm.
  • A nautical mile is the standard international unit from measuring distances travelled by ships and aeroplanes 1 nautical mile (nm) = 1 .853 km
• If an arc of a great circle subtends an angle θ at the centre of the earth,the arcs length is (60 x θ) nautical miles.

Example

A and B on the Earth's surface have an angular distance of 63o. Calculate the great circle distance between A and B, correct to the nearest kilometre. The radius of the Earth is 6400 km.

Solution
AB = θ  x 2πr
       360
= 63 x 2 x π x 6400 = 7037.1675.
   360
= 7037 km

Example

Beijing, China and Perth, Australia have coordinates (40°N, 116°E) and (32°S, 116°E) respectively.

1. What great circle joins Beijing and Perth?
2. What is the angular distance between these two cities?
3. Hence, calculate the shortest distance between Beijing and Perth, to the nearest kilometre, given that the Earth's radius is 6400 km.

Solution

1. The 116°E meridian of longitude.
2. Angular distance = 40° +32° = 72°
3. Distance = 72 x 2π  x 6400
                   360
   = 8042.4772...
   = 8042 km

Example

Find the distance between points P( 40 ⁰ N ,50 ⁰ E ) and Q (20 ⁰ 30 ' S, 50 ⁰ E) and express it in;

1. Nm
2. Km ( Take radius of the earth to be 6370 km )

Solution

1. Angle subtended at the centre is 40 0 + 20.5 ⁰ = 60.5 ⁰
   1 ⁰ Is subtended by 60 nm
   60.5 ⁰ Is subtended by; 60 x 60.5 = 3630 nm
2. The radius of the earth is 6370 km
   Therefore, the circumference of the earth along a great circle is;
   2πr = 6370 x 2 x 22
                               7
   Angle between the points is 60.5 ⁰ .Therefore, we find the length of an arch of a circle which subtends an angle of 60.5 ⁰ at the centre is 360 ⁰ is subtended by arc whose length is
   6370 x 2 x 22
                     7
   Therefore, 60. 5 ⁰ Is subtended by; 60.5 x 6370 x 2 x 22= 6729 km
                                                       360                      7

Example

Find the distance between points A ( 0 0 ,30 0 E ) and (0 0 ,50 0 E) and express it in ;

1. Nm.
2. Km(Take the radius of the earth to be 6370 km)

Solution

1. The two points lie on the equator, which is great circle. Therefore ,we are calculating distance along a great circle.
   Angle between points A and B is ( 50 ⁰ −  30 ⁰ ) = 20 ⁰
2. Distance in km = 20 x 6370 X 2 X 22 = 2224 km
                              360                    7

Distance along a Small Circle (Circle of Latitude)

Example

Find the distance in kilometers and nautical miles between two points ( 30 ⁰ N 45 ⁰ E) and Q ( 30 ⁰ N 60 ⁰ W) .

Solution

Figure a shows the position of P and Q on the surface of the earth while figure b shows their relative positions on the small circle is the centre of the circle of latitude 30 0 N with radius r.
The angle subtended by the arc PQ centre C is 45 ⁰ + 60 ⁰ = 105 ⁰ .So, the length of PQ
= 105 × 2πr
   360

= 105 × 2πRcos 30 ⁰ km
   360
= 105 × 2× 22 × 6370Cosθ km
   360          7
= 10113 km
The length of PQ in nautical miles
= 60 x 105 cos30 ⁰ nm
= 60 x 105 x 0.8660 nm = 5456 nm

In general, if the angle at the centre of a circle of latitude θ is α, then the length of its arc is 60 αcos θ nm, where α is the angle between the longitudes along the same latitude.

Shortest Distance Between Two Points on the Earths Surface

• The shortest distance between two points on the earths surface is that along a great circle.

Example

P and Q are two points on latitude 50 0 N. They lie on longitude 40 0 W and 132 E 0 respectively. Find the distance from P to Q :

1. Along a parallel of latitude
2. Along a great circle

Solution

The positions of P and Q on earths surface are as shown below

1. The length of the circle parallel of latitude 50 0 N is 2 πr km, which is 2 πRcos50 0 km .The difference in longitude between P and Q is 132 ⁰ + 48 ⁰ = 180 ⁰
   PQ = 180 × 2 ×22 × 6370 cos 50^o = 12869 km
          360          7
2. The required great circle passes via the North Pole. Therefore, the angle subtended at the centre by the arc PNQ is;
   = 180 ⁰ – 2 x 50 ⁰ = 80 ⁰
   
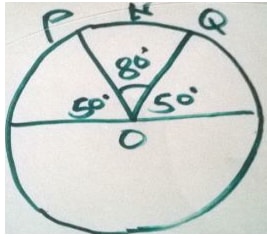
   Therefore the arc PNQ
   = 80 × 2 πR
      360
   = 80 × 2 × 22 × 6370 = 8898 km
     360           7

Note;

Notice that the distance between two points on the earth's surface along a great circle is shorter than the distance between them along a small circle

Longitude and Time

• The earth rotates through 36 0 0 about its axis every 24 hours in west – east direction.Therefore for every 1 0 change in longitude there is a corresponding change in time of 4 minutes, or there is a difference of 1 hour between two meridians 15 ⁰ apart.
• All places in the same meridian have the same local time. Local time at Greenwich is called Greenwich Mean Time, GMT. All meridians to the west of Greenwich Meridian have sunrise after the meridian and their local times are behind GMT.
• All meridian to the east of Greenwich Meridian have sunrise before the meridian and their local times are ahead of GMT. Since the earth rotates from west to east, any point P is ahead in time of another point Q if P is east of Q on the earth's surface.

Example
Find the local time in Nairobi ( 1 ⁰ S,37 ⁰ E ), when the local time of Mandera (Nairobi ( 4 ⁰ N ,42 ⁰ E ) is 3.00 pm
Solution
The difference in longitude between Mandera and Nairobi is ( 42 ⁰ - 37 ⁰ ) = 5 ⁰ , that is Mandera is 5 ⁰ east of Nairobi .
Therefore their local time differ by; 4 x 5 = 20 min.
Since Nairobi is in the west of Mandera, we subtract 20 minutes from 3.00 p.m. This gives local time for Nairobi as 2.40 p.m.

Example
If the local time of London ( 52 ⁰ N,0 ⁰ ), is 12.00 noon, find the local time of Nairobi ( 1 ⁰ S,37 ⁰ E ),
Solution
Difference in longitude is ( 37 ⁰ + 0 ⁰ ) = 37 ⁰
So the difference in time is 4 x 37 min = 148 min
= 2 hrs. 28 min
Therefore , local time of Nairobi is 2 hours 28 minutes ahead that of London that is,2.28 p.m

Example
If the local time of point A ( 0 ⁰ N,170 ⁰ E ) is 12.30 a.m, on Monday,Find the local time of a point B ( 0 ⁰ N,170 ⁰ W ).
Solution
Difference in longitude between A and B is 170 ⁰ + 170 ⁰ = 340 ⁰
In time is 4 x 340 = 1 360 min
= 22 hrs. 40 min.
Therefore local time in point B is 22 hours 40 minutes behind Monday 1 2:30 p.m. That is, Sunday 1 .50 a.m.

Speed

• A speed of 1 nautical mile per hour is called a knot. This unit of speed is used by airmen and sailors.

Example

A ship leaves Mombasa ( 4 ⁰ S,39 ⁰ E) and sails due east for 98 hours to appoint K Mombasa ( 4 ⁰ S,80 ⁰ E) in the indian ocean.Calculate its average speed in;

1. Km/h
2. Knots

Solution

1. The length x of the arc from Mombasa to the point K in the ocean
   41 x 2πr
   360
   = 41 x 2πRcos 4 ⁰ km
     360
   = 41 x 2 x 22x 6370 cos 4 ⁰ km= 4549 km
     360         7
   Therefore speed is = 4549 = 46.41 km/h
                                   98
2. The length x of the arc from Mombasa to the point K in the ocean in nautical miles
   x = 60 x 41 x cos4 0 nm
   = 60 x 41 x 0.9976 nm = 2454 nm
   Therefore , speed = 2454
                                  98
   = 25.04 knots

Past KCSE Questions on the Topic

1. An aeroplane flies from point A (1 ⁰ 15'S, 37 ⁰ E) to a point B directly North of A. the arc AB subtends an angle of 45 ⁰ at the center of the earth. From B, aeroplanes flies due west two a point C on longitude 23 0 W.)(Take the value of π = ²² / ₇ as and radius of the earth as 6370km)
   1. 
      
      1. Find the latitude of B
      2. Find the distance traveled by the aeroplane between B and C
   2. The aeroplane left at 1 .00 a.m. local time. When the aeroplane was leaving B, what was the local time at C?
2. The position of two towns X and Y are given to the nearest degree as X (45 ⁰ N, 10 ⁰ W) and Y (45 ⁰ N, 70 ⁰ W)
   Find
   1. The distance between the two towns in
      1. Kilometers (take the radius of the earth as 6371 )
      2. Nautical miles (take 1 nautical mile to be 1 .85 km)
   2. The local time at X when the local time at Y is 2.00 pm.
3. A plane leaves an airport A (38.5 ⁰ N, 37.05 ⁰ W) and flies dues North to a point B on latitude 52 ⁰ N.
   
   1. Find the distance covered by the plane
      
   2. The plane then flies due east to a point C, 2400 km from B. Determine the position of C
      Take the value π of as ²² / ₇ and radius of the earth as 6370 km
      
4. A plane flying at 200 knots left an airport A (30 ⁰ S, 31 ⁰ E) and flew due North to an airport B (30 ⁰ N,31 ⁰ E)
   
   1. Calculate the distance covered by the plane, in nautical miles
   2. After a 15 minutes stop over at B, the plane flew west to an airport C (30 ⁰ N, 13 ⁰ E) at the same speed.
      Calculate the total time to complete the journey from airport C, though airport B
5. Two towns A and B lie on the same latitude in the northern hemisphere. When its 8 am at A, the time at B is 11.00 am.
   1. Given that the longitude of A is 15 ⁰ E find the longitude of B.
      
   2. A plane leaves A for B and takes 3 ¹ / ₂ hours to arrive at B traveling along a parallel of latitude at 850 km/h. Find:
      1. The radius of the circle of latitude on which towns A and B lie.
      2. The latitude of the two towns (take radius of the earth to be 6371 km)
6. Two places A and B are on the same circle of latitude north of the equator. The longitude of A is118 ⁰ W and the longitude of B is 133 ⁰ E. The shorter distance between A and  the circle of latitude is 5422 nautical miles. Find, to the nearest degree, the latitude on which A and B lie B measured along
7. A plane flies by the short estimate route from P (10 ⁰ S, 60 ⁰ W) to Q (70 ⁰ N, 120 ⁰ E) Find the distance flown in km and the time taken if the aver age speed is 800 km/h. Calculate the distance in km between two towns on latitude 50 0 S with long longitudes and 20 0 W. (take the radius of the earth to be 6370 km)
8. Calculate the distance between M (30 ⁰ N, 36 ⁰ E) and N (30 ⁰ N, 144 ⁰ W) in nautical miles.
   1. Over the North Pole
   2. Along the parallel of latitude 30 ⁰ N
9. 
   
   1. A ship sailed due south along a meridian from 12 ⁰ N to 10 ⁰ 30'S. Taking the earth to be a sphere with a circumference of 4 x 10 4 km, calculate in km the distance traveled by the ship.
   2. If a ship sails due west from San Francisco (37 ⁰ 47'N, 122 ⁰ 26'W) for distance of 1320 km. Calculate the longitude of its new position (take the radius of the earth to be 6370 km and π = 22/7)

---

Want to Improve Your Grade?

Guaranteed, improve your overall grade from D- to C+, C- to B+, or B plain to A plain, using our updated and fresh content.

Thousands of subscribed students and teachers country-wide rely on our content, which is updated weekly, with the latest past papers and revision notes.

Top performing schools and students regularly use our materials. We receive numerous "Thank you notes" after every KCSE Exams.

---

Don't Be Left Out.

Subscribe Today!

Choose among the three options below.

Higher Target Plan

• Unlimited PDF Downloads
• Unlimited Notes Downloads
• Unlimited Past Papers Downloads
• No Ads

Achiever's Plan

• Unlimited PDF Downloads
• Unlimited Notes Downloads
• Unlimited Past Papers Downloads
• No Ads

Not Yet Convinced?

Read Customer Reviews

• Z

  " It's the best app to all candidates for notes, questions and even answers. It has helped me improve notably in my exams... "

  Zahra Bandal

  Form 4 Student - Mombasa

• F

  " You guys are the best you totally fulfilled my expectations cause I really like this app cause 1: Subjects are well presented 2: The notes range from Form 1 to 4 This app really helps especially to a person who does not have study books. "

  Faith Mwande

  Form 3 Student - Kitale

• B

  " I love this site, it has all the revision materials and notes that I need, to teach and sharpen my students, for improved grades in exams. I also get teaching aids like Schemes of work, conveniently and therefore I save a lot of time... "

  Belinda Akinyi

  English Teacher - Nairobi

Read 8403 times Last modified on Monday, 05 October 2020 07:07

Print PDF for future reference Join our whatsapp group for latest updates

Longitude And Latitude In Mathematics Pdf

Source: https://www.easyelimu.com/high-school-notes/maths/form-4/item/1378-longitudes-and-latitudes

Posted by: wardsleve2000.blogspot.com

Share this post